Galileo y la medida de la gravedad.

Galileo y la determinación de la gravedad

Tras haber leído el capítulo 3 del libro “De Arquímedes a Einstein”, vamos a reproducir el experimento de la caída libre de los cuerpos de Galileo, complementándolo con gráficas, cálculos y tablas. Hallaremos la gravedad y la velocidad de la bola utilizando las fórmulas de la energía.

En primer lugar, anotaremos los datos que nos han facilitado Ángel y Víctor en una tabla (Debido a que no es posible calcular la velocidad instantánea de cada punto con los medios que disponemos, haremos una aproximación: calcularemos la velocidad media de cada intervalo):

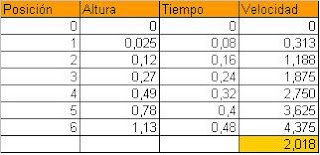
Basándonos en la tabla anterior, hemos confeccionado la siguiente gráfica, que muestra la variación de la altura de las bolas respecto al tiempo:

En esta gráfica se observa que el resultado es una línea curva que nos indica que estamos ante un movimiento rectilíneo uniformemente acelerado (MRUA). Con esta observación nos ponemos a favor de Galileo, quien intentó demostrar que Aristóteles se equivocaba, ya que el creía que el movimiento debería ser rectilíneo uniforme (MRU). Según éste último, el resultado debería ser una línea recta.

A continuación, detallamos otra gráfica que representa la variación de la velocidad respecto al tiempo:

Utilizando la fórmula de la aceleración, calcularemos el valor de la gravedad:

a=(4,375m/s-0,313m/s) / (0,48 s-0,08 s)
a= (4,062 m/s) / (0,40s)
a=10,155 m/s2

Aunque el valor de la gravedad no es del todo correcto, si podemos decir que es bastante aproximado, sólo hay un margen de error de 0,355, seguramente debido a errores en la toma de datos, recordamos que el ser humano no es una máquina de medir perfecta. Tenemos una hipótesis sobre la causa de este pequeño error, pude deberse al rozamiento que produce el aire a la bola.

Utilizando la teoría de la conservación de la energía, podemos averiguar la velocidad que tendrá la bola en el punto 6 ( v6). Dicha teoría explica que la suma de las energías (cinética y potencial) de un cuerpo debe ser constante a lo largo de un recorrido siempre que no haya fuerzas no-conservativas (como, por ejemplo, el rozamiento). En nuestro caso, debido a que el rozamiento queda prácticamente anulado, la energía mecánica se debería mantener.

Ec=1/2 mv2
Ep= mgh

-La energía cinética en la posición inicial es nula pues la velocidad es 0.
-La energía potencial en la posición final también es nula porque la altura en ese punto es 0.



mgh= mgh´ + 1/2mv^2
9.8(h-h´)=1/2v^2
9.8 . 1,13= 1/2v^2
11.07= 1/2v^2
v= 4.706 m/s



Para complementar el cálculo anterior, calcularemos también la velocidad con las ecuaciones cinemáticas.

v= gt v= 9.8 . 0.48 = 4.706 m/s

Ambos datos son iguales, lo cual indica que el experimento ha sido un éxito. Sin embargo, este éxito se lo debemos en plenitud a Galileo Galilei, quien fue capaz de establecer el valor de la gravedad (entre otras muchas cosas) sin siquiera tener referencias sobre este concepto. Se le añade mérito al experimento de Galileo si decimos que no tuvo unos medios precisos para llevarlo a cabo, utilizó un laúd para tomar los tiempos de caída.

Capítulo 3- Galileo Galilei

RESUMEN:
A Galileo le costó entrar en el mundo profesional, aún así el estudiaba/ inventaba de una forma increíble, hasta que por fin a los 25 años consiguió entrar en la universidad de Pisa, aunque su salario no era de los mejores. Al mismo tiempo que enseñaba, estudiaba el enfoque que había dado Arquímedes al movimiento, llegando a la conclusión de que dos cuerpos se aceleran de la misma forma aun teniendo la misma masa, enfrentándose a la teoría de Aristóteles, que decía que la aceleración de un cuerpo es proporcional al de su masa, haciendo el famoso experimento de tirar varias bolsas rellenas de diferente cosas desde lo alto de la torre de Pisa, así , aunque no cayeron justo al mismo tiempo, se pudo apreciar que la velocidad que alcanzaban no era proporcional a su peso.
Al cabo del tiempo, tras una serie de cálculos y experimentos, concluyó que el universo no era inmutable y que la Tierra giraba alrededor del Sol, y no al revés, sin embargo decidió no seguir predicando esa idea pues empezaba a tener miedo a la iglesia. Todo continuó más o menos igual hasta que “inventó” el telescopio(le hizo algunas mejoras muy importantes), le doblaron es sueldo y empezó a estudiar el cosmos, descubriendo multitud de nuevos astros, escribió un libro donde reunía todos sus nuevos descubrimientos, este libro le otorgó una gran fama y privilegio, tanto que le hizo trasladarse a la Toscana.
En los años posteriores, empezó a defender cada vez más públicamente la postura heliocéntrica de Copérnico, alegando por ejemplo, que se puede demostrar que la Tierra no es está quieta gracias a las mareas, como explicó a un cardenal en una de sus cartas.
Al defender las cada vez más argumentadas posturas del sistema Heliocéntrico, la Iglesia empezó a centrarse en el, ya que estas ideas según la mayoría eclesiástica iban en contra de la Biblia, y se las consideraba una herejía, así la inquisición empezó a llamarle a juicio, y él cada vez estaba más asustado, pero por suerte se veía defendido por el nuevo Papa Urbano VIII.
Así consiguió vivir durante unos años, hasta la publicación de su obra “los diálogos” (en la que se burla completamente del geocentrismo de Ptolomeo). En este momento, 1663, Urbano le traiciona aliándose con los enemigos de Galileo y le lleva a juicio en Roma. En este juicio se prohíbe la venta de el libro, pero además se le condena a no más que una serie de rezos y a admitir públicamente que estas ideas son tremendamente erróneas, argumentando que la Tierra no gira alrededor del Sol, si no al revés, aunque cuenta la leyenda que tras terminar el discurso, dice “y sin embargo, se mueve”…
Meses después le vuelven a llamar a juicio, lo intenta evitar realizando una conferencia en la que vuelve a explicar que sus ideas son falsas, pero le vuelven a condenar a cadena perpetua en un palacete.
Aquí encuentra tiempo para seguir estudiando, y apreciando las artes, hasta que le llega la terrible noticia de que una de sus hijas había contraído una gravísima enfermedad, por lo cual pidió permiso para poder trasladarse temporalmente cerca de su hija, y consigue el permiso.En este lugar se dedica a acompañar a su hija, y a seguir estudiando astronomía, y escribe un libro en el cual fulmina con la física aristotélica, y establece las bases de la mecánica. Unos días más tarde muere, un 8 de enero de 1642, a los 78 años de edad y ciego de los dos ojos.

VALORACIÓN PERSONAL:
En este capítulo me parece que se refleja muy bien como la iglesia, en vez de intentar que el ser humano viva en un mundo mejor, lo único que buscaban era el poder, y le defendían incluso matando a científicos tan buenos y brillantes como Giordano Bruno(por ejemplo). El capítulo es muy interesante y sobre todo muy educativo puesto que así la gente que lo lea sabrá las barbaridades que ha hecho la iglesia a lo largo de la historia con excusa de que defendían la fe cristiana. En general es interesante como cuenta desde un punto de vista neutral la vida de Galileo, toda su obra y todos sus logros.

Capítulo 3: Galileo. La caída libre de los cuerpos.

Introducción

En este capítulo del libro De Arquímedes a Einstein leeremos una descripción detallada de la vida de Galileo Galilei a modo de biografía y otra descripción de su experimento mas característico: La caída libre de los cuerpos. Pero vayamos paso a paso.

Biografía

Galileo Galilei fue un célebre astrónomo, filósofo, matemático y físico nacido en Pisa en el año 1564 en el seno de una familia numerosa y acomodada. Galileo fue el primero de siete hermanos, todos ellos bautizados en la catedral de Pisa. Vivió en la época del renacimiento, época que resulta muy complicada para todos los científicos del momento. Esto se debe a que, a pesar de que el renacimiento busca la revitalización cultural (artística y científica) de la Europa Occidental, la religión seguía teniendo una gran importancia. Fueron muchos los que murieron quemados por la Inquisición por cuestionar el dogma de la Iglesia Católica. Sin embargo, Galileo recibió el apoyo del Papa Urbano VIII. Entonces Galileo escribe una polémica obra (el Diálogo) en la que se burla de la teoría geocéntrica de Ptolomeo, en vez de crear una obra objetiva. Ésto hace enfadar a Urbano VIII quien le amenaza con la tortura. Finalmente, Galileo cede.

Obra

Probablemente, Galileo Galilei sea mundialmente conocido por su gran aportación en la mejora del telescopio (lo cual propicia que Galileo formule unos años mas tarde la teoría heliocéntrica). Sin embargo, en el libro De Arquímedes a Einstein se da más importancia al experimento que realizó desde la torre de Pisa en el cual dejó caer bolas diferentes en masa, tamaño y material desde lo alto de la susodicha torre. Este experimento queda justificado por el constante interés de Galileo de cuestionar las teorías de Aristóteles. El resultado del experimento es que las bolas no caian a la vez pero sí muy cerca temporalmente, lo cual demostró que la teoría aristotélica era falsa (el tiempo de vuelo no dependía del peso de la bola)

Para aumentar la precisión del experimento, Galileo repitió el experimento sobre un plano inclinado en vez de en caída libre, con lo que eliminaba el rozamiento y así pudo averiguar la aceleración de la gravedad.

Valoración Personal

Este capítulo me ha parecido muy interesante en el sentido de que la vida y la obra de Galileo deberían ser conocidos a escala mundial y no solo como un trabajo de física. Por tanto me parece que la labor de Manuel Lozano Leyva es admirable, ya que utiliza este libro como un medio para difundir la historia de tan importante científico. Opino que debería servir como ejemplo para otros escritores. Centrándome más en el capítulo en sí, me parece que la biografía de Galileo Galilei debería ser quizá algo menos detallada ya que este libro es de carácter científico más que histórico. A pesar de este pequeño detalle, me parece que está muy bien redactado y que, una vez más, incita a los lectores a reproducir el experimento mediante explicaciones e ilustraciones.

En definitiva, otro buen capítulo que hacen de este libro un imprescindible para comprender la historia de la física.

CAPITULO 2

(Perdon que se me ha olvidado poner el número del capítulo y quizas asi mi profesor Victor sepa de que capítulo del libro estoy hablando, gracias por su comprension).

DE ARQUÍMEDES A EINSTEIN

En la antigüedad los científicos eran mucho mas valorados que ahora puesto que antes estos no solo se especializaban en una cosa sino que dominaban varios aspectos como las matemáticas, la poesía o la filosofía.
Estos además también tenían otro nombre, se les llamaban sabios, pues comparados con el resto de la población eran casi como dioses.
También había enormes bibliotecas con miles de manuscritos y pergaminos aunque la mayoría desaparecieron en guerras o en catástrofes.
La mas importante es la de Alejandría, de la cual el director fue nuestro querido sabio Eratóstenes.
De este hombre es el que voy a hablaros puesto que el fue el primero que dedujo que la tierra es redonda. Este acto tiene mucho merito pues en la época ni se planteaba esta hipótesis. La idea le vino en un día de verano en el cual ningún edificio daba sombra en la ciudad de Asuán por lo que el sol estaba exactamente encima. El dedujo que esto seria a causa de que o el sol o la tierra se movían.
El experimento que llevo a cabo fue el siguiente:
Cuando se dio cuenta de este fenómeno dedujo que se podía calcular la circunferencia de la tierra así que todos los mercaderes que ese año viajaron de Alejandría hasta Asuán tendrían el deber de contar de diferente manera(vueltas de rueda de carro, pasos, etc)la distancia entre estas dos ciudades. Sus cálculos finales le dieron mas o menos 250000 estadios. Estuvo muy cerca de acertar aunque cometió algunos errores que hubiera echo cualquier otra persona, su margen de error fue se un 1,5% aunque parezca muy increíble.
A mi me parece que esta acción demuestra lo creativo y lo ingenioso que puede llegar a ser el ser humano. Hay que tener también muy en cuenta que en esa época no se podía medir nada exactamente.
Me a parecido un capitulo interesantísimo y me a gustado mucho. Espero que el numero tres me guste tanto o mas que este.

Capítulo 2: Eratóstenes y la medida del radio de la Tierra

Biografía de Eratóstenes

Eratóstenes fue un matemático, astrónomo y geógrafo de origen griego que nació en el año 276 a.C. y murió en el año 194 a.C. Este genio fue amigo del célebre Aristóteles, lo cual refuerza el hilo conductor de la obra (Aristóteles aparece en el capítulo anterior). Estudió en Atenas. Debido al rápido prestigio que adquirió, fue llamado a Alejandría para hacerse cargo de la Biblioteca, lugar en el cual continuó con sus estudios y que ocupó hasta su muerte. Fue en esta ciudad precisamente donde realizó el experimento por el cual es conocido: la medida del radio de la Tierra.

Análisis

Como es de esperar, este capítulo nos habla del descubrimiento Eratóstenes. Ésto supuso uno de los descubrimientos más importantes de toda la historia.

Analizando el contenido de éste capítulo, se puede apreciar que el tema principal es el gran descubrimiento de Eratóstenes, pero, además de eso, el autor, Manuel Lozano Leyva, ha tratado otros aspectos diferentes pero relacionados con este tema, como por ejemplo, el cambio de las estaciones a lo largo del año, meridianos y paralelos,y la longitud y la latitud. Me fijé sobre todo en el primero. El autor introduce este tema por medio de una pregunta: ¿Por qué hace frío en invierno y calor en verano? Hasta el día de hoy pensaba que era una respuesta mas o menos obvia, pero me sorprendió que existieran profesores de universidad que no sepan la respuesta. O peor, que no sea sensata. La respuesta a la pregunta sería, a grandes rasgos, que es una consecuencia de la inclinación del eje terrestre. Cuanto mas perpendiculares lleguen los rayos del sol a la superficie terrestre, más calor.

Analizando el tema principal nos encontramos con que la medida del radio de la tierra no es un experimento complejo (o al menos eso es lo que nos quiere transmitir el autor) sino que parece impensable que se descubriera en esa época. Eratóstenes comparó la sombra que proyectaban dos varas de misma longitud en dos ciudades de misma latitud: Alejandría y Siena. Para ésto midió la distancia entre las dos ciudades. Eratóstenes concluyó que la circunferencia de la Tierra debería ser 39.375 kilómetros.

Valoración personal

¡¡ 1,5 % !! Cuesta creerlo pero el número que he puesto a la izquierda es el porcentaje de error que cometió Eratóstenes en su resultado final. Teniendo en cuenta los escasos medios que disponía en aquella época, hay que decir que tiene mucho mérito. Sin embargo no todos aceptaron este descubrimiento. A finales del siglo XV, Cristóbal Colón intentó razonar que el radio era en verdad mucho menor que el que estableció Eratóstenes con el fin de que le financiaran el viaje a las Indias, y como ya todos sabemos acabó descubriendo América. Me parece que, a pesar del sorprendente éxito de la expedición de Colón, todos deberían haber aceptado a Eratóstenes como un auténtico genio por el ingenioso procedimiento que utilizó.

actividad 1 portada del libro

Análisis de la portada:
Este libro ha sido elegido por expertos en el arte de la educación y para ello tienen que cuidar todos los detalles para que atraigan a los jóvenes estudiantes, como por ejemplo la portada del libro.
El libro en si describe los experimentos más famosos donde se encuentran Eratóstenes o Galileo.
El libro contiene diez experimentos que son:
1)Interferencia de los electrones al pasar por una doble rejilla.
2)Caída libre de los cuerpos.
3)Determinación de la carga del electrón con gotas de aceite.
4)Descomposición de la luz del sol por un prisma.
5)Interferencia de la luz.
6)Medida de la gravedad con una balanza de torsión.
7)Medida de la circunferencia de la Tierra.
8)Caída de los cuerpos en planos inclinados.
9)Descubrimiento del núcleo atómico.
10)El péndulo de Foucault.
Fueron elegidos mediante una encuesta que se fue publicando en los periódicos del mundo entero preguntando a la gente cual experimento pensaban que era el más bello de toda la historia de la tierra.
Algunos de los experimentos que nombra y describe el libro ya me resultan conocidos pues se habla de ellos en la vida diaria. Sabemos que el principio de la hidrostática fue enunciado por Arquímedes, un científico cronológicamente opuesto a Einstein, lo cual nos indica que el libro va a hacer un viaje a través de la Historia parándose en los científicos de mayor prestigio.

Manuel Lozano Leyva (el autor) es un catedrático en la Universidad de Sevilla y un científico del departamento de Física Atómica, Nuclear y Molecular. Además de diversas ayudas a la consolidación del grupo de investigación FQM-160, grupos de la Junta de Andalucía (de donde él es), ha participado en diversos proyectos como la medida de datos nucleares relevantes para física nuclear básica y transmutación de residuos radiactivos o teorías de muchos cuerpos para sistemas de fermiones fuertemente correlacionados.